Software: Thruster Firing Command - Remainder
Description
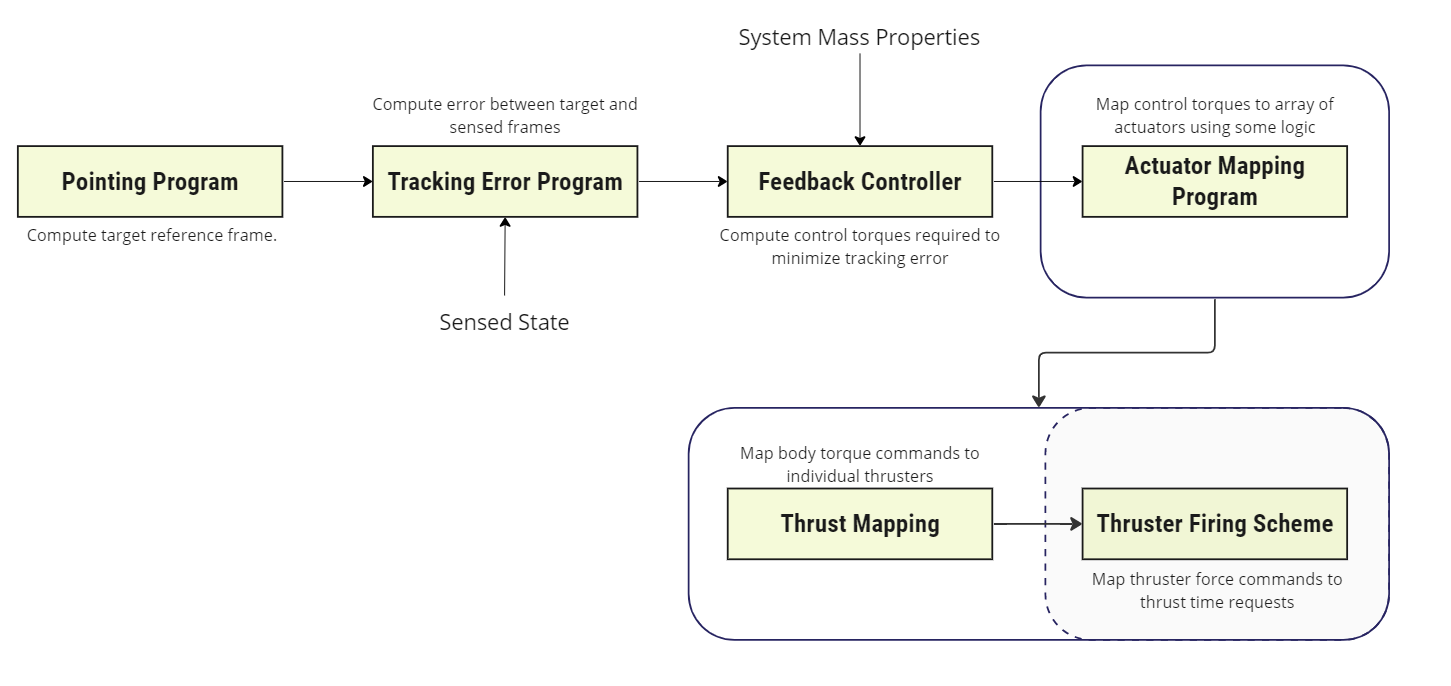
This module is designed to be used as part of an actuator mapping program, as illustrated above. Given an array of thrust force requests \(\mathbf{F}\), this model attempts to map these requests to fire commands. This is required because the default Thruster module requires a fire time (begin) and duration as command inputs. Further, thrusters may implement minimum firing durations along with thrust ramps on and off curves. They do not implement instantaneous impulses. Further, if a thruster is currently firing, it will not accept a new thruster firing command. As a result, a firing scheme is required that implements logic that maps the input force requests to finite thruster firing times. The scheme implemented here corresponds to the Remainder model in [1].
Example Use Cases
- RCS Firing Scheme: corresponds to implementing an RCS thruster firing scheme. This is just one example of a firing scheme. Explore different firing schemes to optimize system performance.
Module Implementation
As discussed in [1] and considering only a single thruster, the level of thruster activity relative to its maximum duty cycle (\(\mathcal{l}\)) can be described as,
Here \(T_p\) is the desired pulse duration, \(\Delta t\) is the control update period, and \((\mathbf{r}_t - \mathbf{r}_{CmB})\) is the distance between the thruster and the spacecraft’s centre of mass, \(\hat{\mathbf{g}}_t\) is the unit thrust vector and \(F_{nom}\) is the nominal thrust output during steady-state operations.
Rearranging for \(T_p\) gives,
In other words, the firing time \(T_p\) required to achieve the desired torque over the control period (i.e. simulation time step) is the ratio of desired force to maximum. However, if the resulting firing time is less than the minimum possible firing time (\(T_{min}\)), then no firing command will be passed to the thruster. This can result in poor/unstable pointing behaviour that is time-step dependent.
To improve stability for the case where \(T_p < T_{min}\), \(T_p\) is accumulated and added to the next step until a \(T_p \geq T_{min}\). Similarly, for cases where \(F_{des}/F_{max} > 1\), a constant factor of \(1.1\Delta t\) is applied to oversaturate the thruster command without creating long-duration firing commands that block future requests as the dynamic state of the system evolves.
References
[1] John Alcorn, Hanspeter Schaub, and Scott Piggott. Steady-state attitude and control effort sensitivity analysis of discretized thruster implementations. AIAA Journal of Spacecraft and Rockets, 54(5):1161{1169, 2017.