Software: Relative Pointing
Description
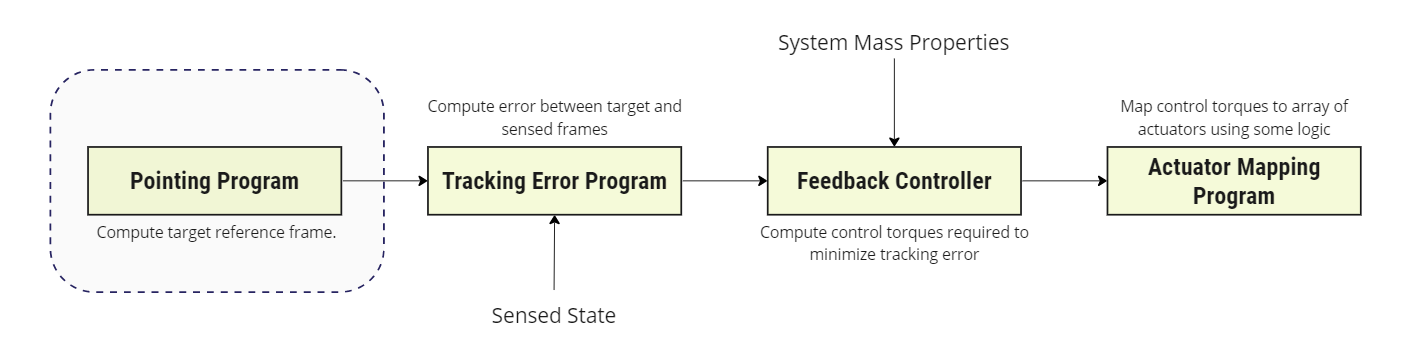
This module is designed to work as the pointing program in an ADCS software chain as shown in the figure below.
This model provides a general method to establish a pointing frame between two known positions. Specifically, this module constructs a reference frame \(\mathcal{R}\) that aligns a vector (\(^\mathcal{B}\mathbf{a}\)) defined by the user in the body frame \(\mathcal{B}\) of the parent object with a vector that points to a target object (\(^\mathcal{B}\mathbf{p}\)) in the body frame.
Example Use Cases
- Space-based Observations: Establish a pointing reference frame between a nearby space object and an on-board sensor.
- Terrestrial Observations: Establish a pointing reference frame between a plane based on received ADS-B (flight tracking) position information.
Module Implementation
The relative pointing frame is constructed about a principle pointing axis, which is derived from the inertial position of the parent spacecraft \(^\mathcal{N}\mathbf{r}_{p}\) and target \(^\mathcal{N}\mathbf{r}_{t}\):
A coordinate system about this principle axis is then built such that:
Where \(\mathbf{\hat{z}} = [0, 0, 1]^T\) and the DCM is \([RN]=[\mathbf{\hat{x}}^T, \mathbf{\hat{y}}^T, \mathbf{\hat{z}}^T]\). The angular velocity of the frame may then simply be calculated from the time-step \(t\) as:
Using this result, and applying equation 3.164 in [1], the angular velocity of the \(\mathcal{R}\) frame with respect to \(\mathcal{N}\) in the \(\mathcal{R}\) frame components may be computed as:
The above definitions will align the reference frame's x-axis with the target. To align with a user-specific vector, we create a second coordinate frame \(R_1\). In the case that the \(\mathcal{B}\) frame aligns with the \(R_1\) frame, \(^\mathcal{B}\mathbf{a}\) has to align with \(^\mathcal{N}\mathbf{p}\). For this reason, an \(\mathcal{A}\) frame is built around the \(^\mathcal{B}\mathbf{a}\) vector, such that:
where all the above are in \(\mathcal{B}\). The resultant DCM \([AB]=[\mathbf{\hat{x}}^T, \mathbf{\hat{y}}^T, \mathbf{\hat{z}}^T]\). Converting to MRPs, the final rotation between \(\mathcal{R}_1\) and \(\mathcal{N}\) is simply:
The angular velocity and angular acceleration remain the same.
References
[1] Hanspeter Schaub and John L. Junkins. Analytical Mechanics of Space Systems. AIAA Education Series, Reston, VA, 3rd edition, 2014.