Editor: Configuring a Satellite Constellation
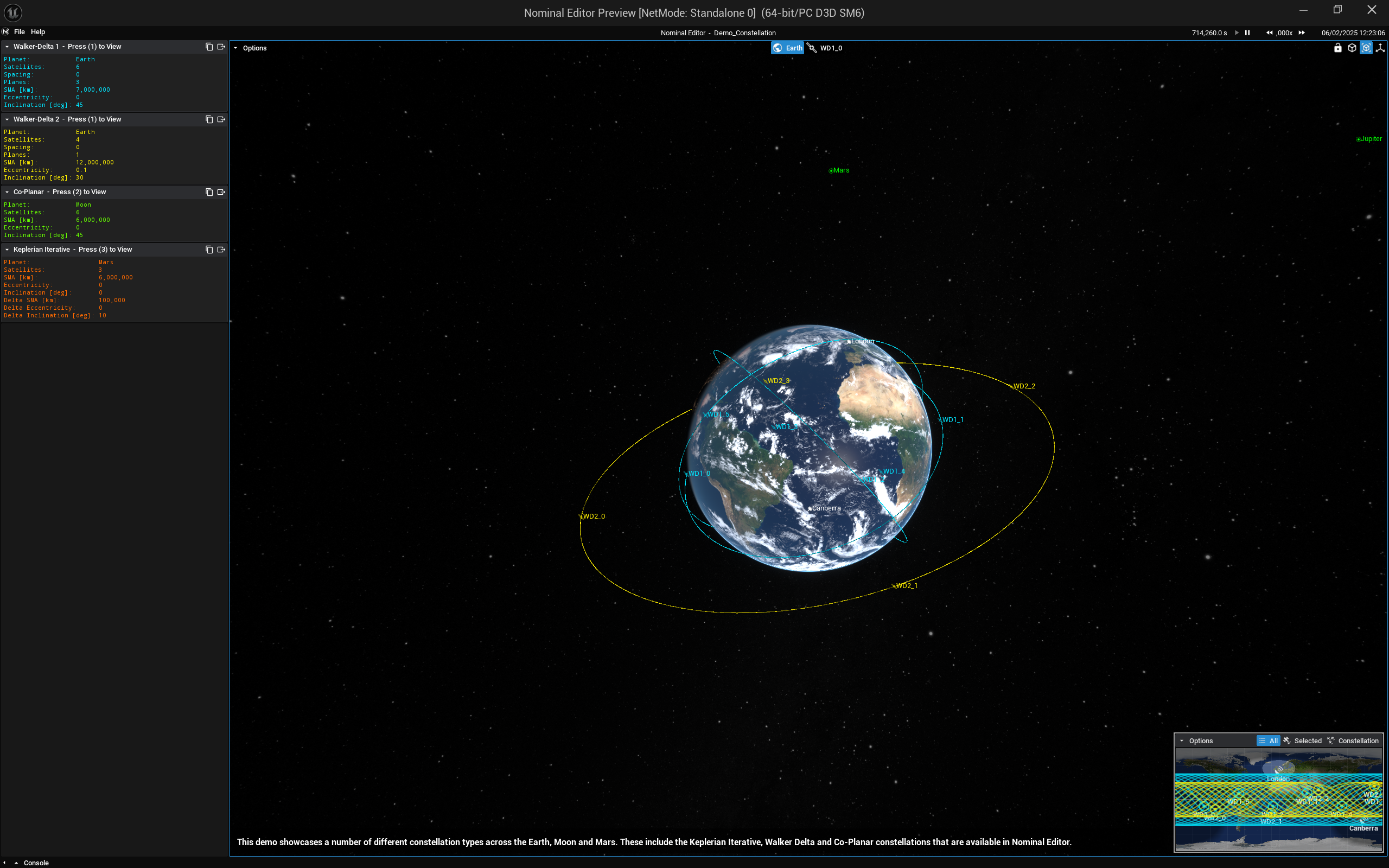
This guide showcases how to instantiate a Walker-Delta, Coplanar and Keplerian Iterative constellation using the provided utility functions. An example of this is in the demo in Orbits/Demo_Constellation. This uses a Walker Delta function to initialize a constellation around the Earth, with spacecraft equally spaced around the orbit. The demo also has a co-planar constellation around the Moon and a Keplerian iterative constellation around Mars.
Walker Delta Constellation
A Walker-Delta constellation is a specific arrangement of multiple communication satellites in a particular orbit. It is designed to provide global coverage and redundancy for satellite-based services, such as telecommunications and broadcasting. The constellation typically consists of a specified plane with satellites spaced equidistantly in each plane.
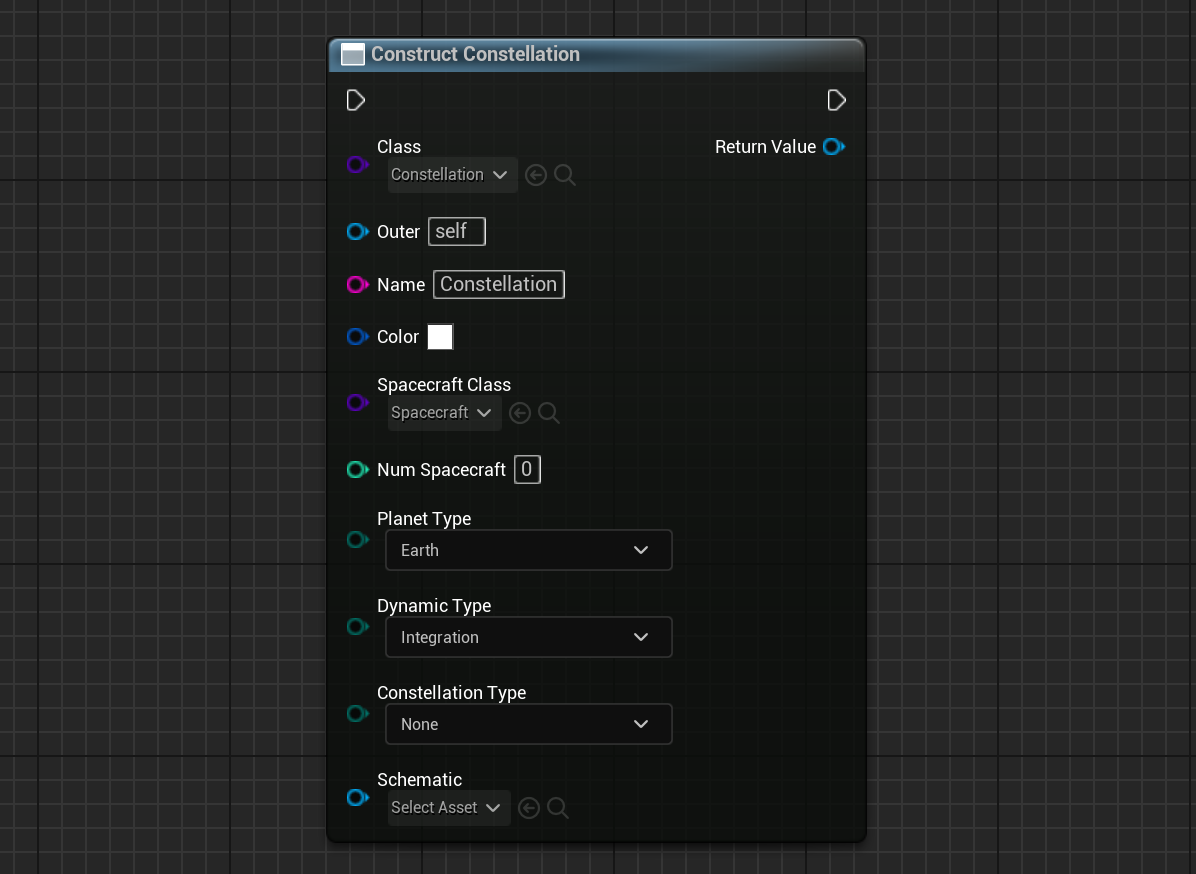
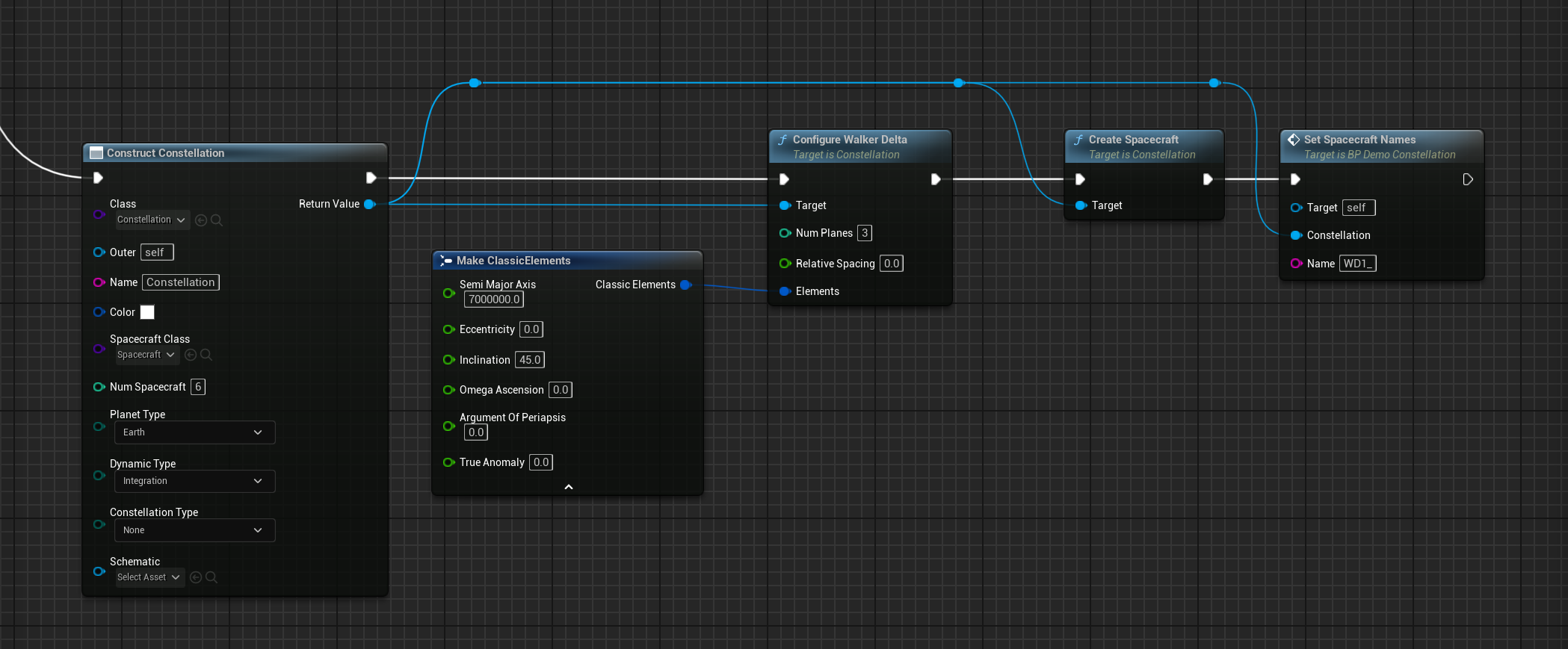
To define the orbits for a Walker-Delta constellation call the Construct Object from Class function and select Constellation as the class. This will create a generic constellation that can configure the constellation’s planet to orbit, the colour of the orbit lines, the blueprint for each spacecraft, the number of spacecraft in the constellation and the dynamic and constellation type. Schematic should be left to its default value.
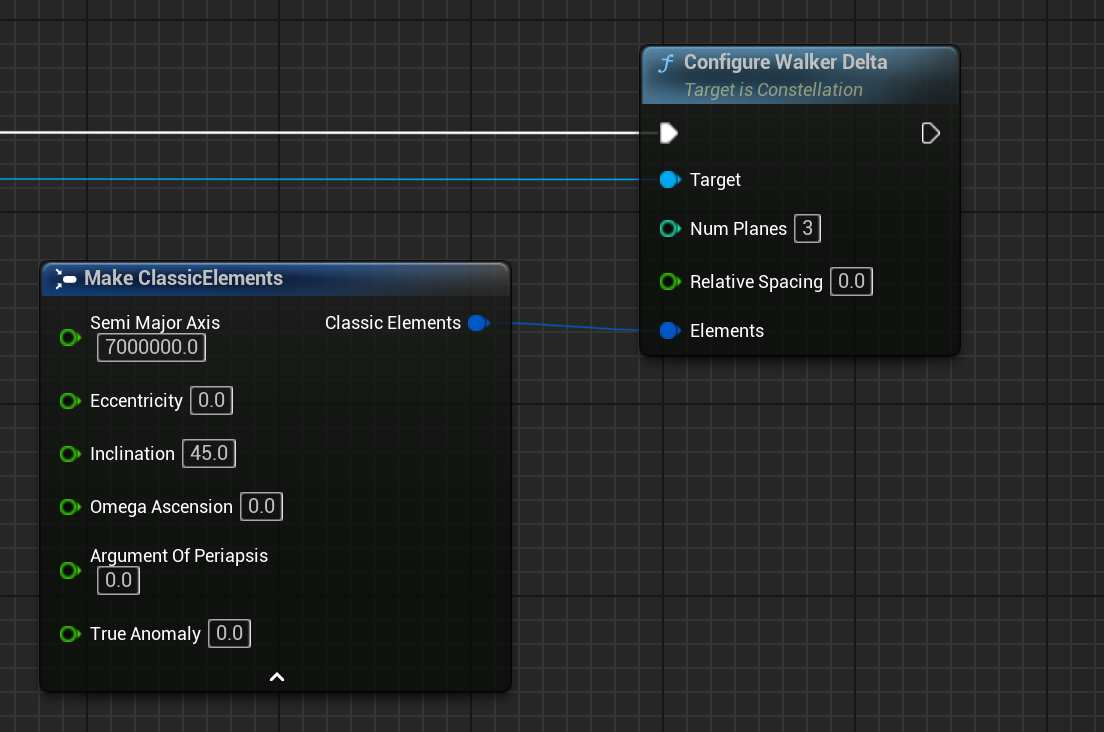
Dragging from the return node of the Construct node, call Configure Walker Delta on the Constellation. This node configures the elements of the first spacecraft in the constellation with the following properties.
- Num Planes: The total number of orbiting planes that should be created. If the plane is set to two, there will be two types of orbits that the satellites will be across. The amount of spacecraft must be able to be divided into the number of planes to be a configurable constellation.
- Relative Spacing: The degree of spacing between each of the spacecraft. This can be used as an override when constructing the constellation. If left at 0, it will evenly space them out.
- Semi-Major Axis: The distance from the centre of the orbiting planet and the constellation (constant for all spacecraft in the constellation).
- Inclination: The inclination angle of the orbit that all spacecraft and orbiting planes should follow.
- Ref: These values provide reference values for the planes initialized which will define where the plane and initial starting points of the spacecraft are on the plane.
Lastly, call Create Spacecraft from the constellation pin to spawn the spacecraft into to simulation. Optionally also call Set Spacecraft Names from the constellation pin to name all the spacecraft. They will all start with the Name inputted and add a number starting from 0 and counting up. E.g. WD1_0, WD1_1, etc.
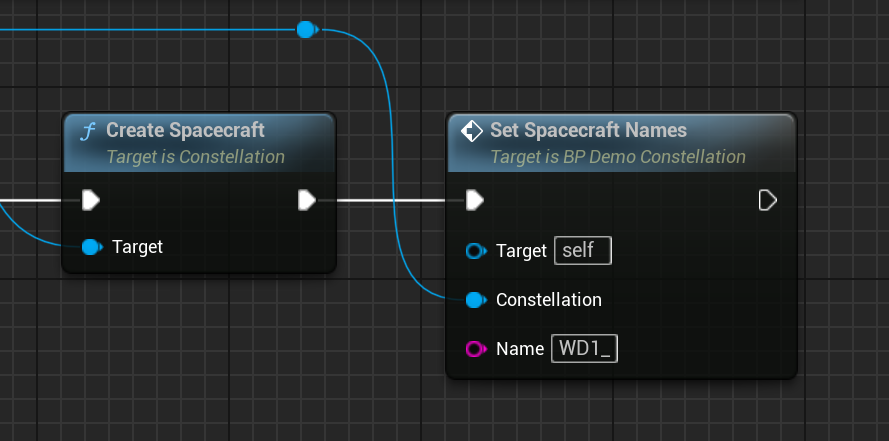
A completed blueprint function of creating a Walker-Delta Constellation would look something like this image.
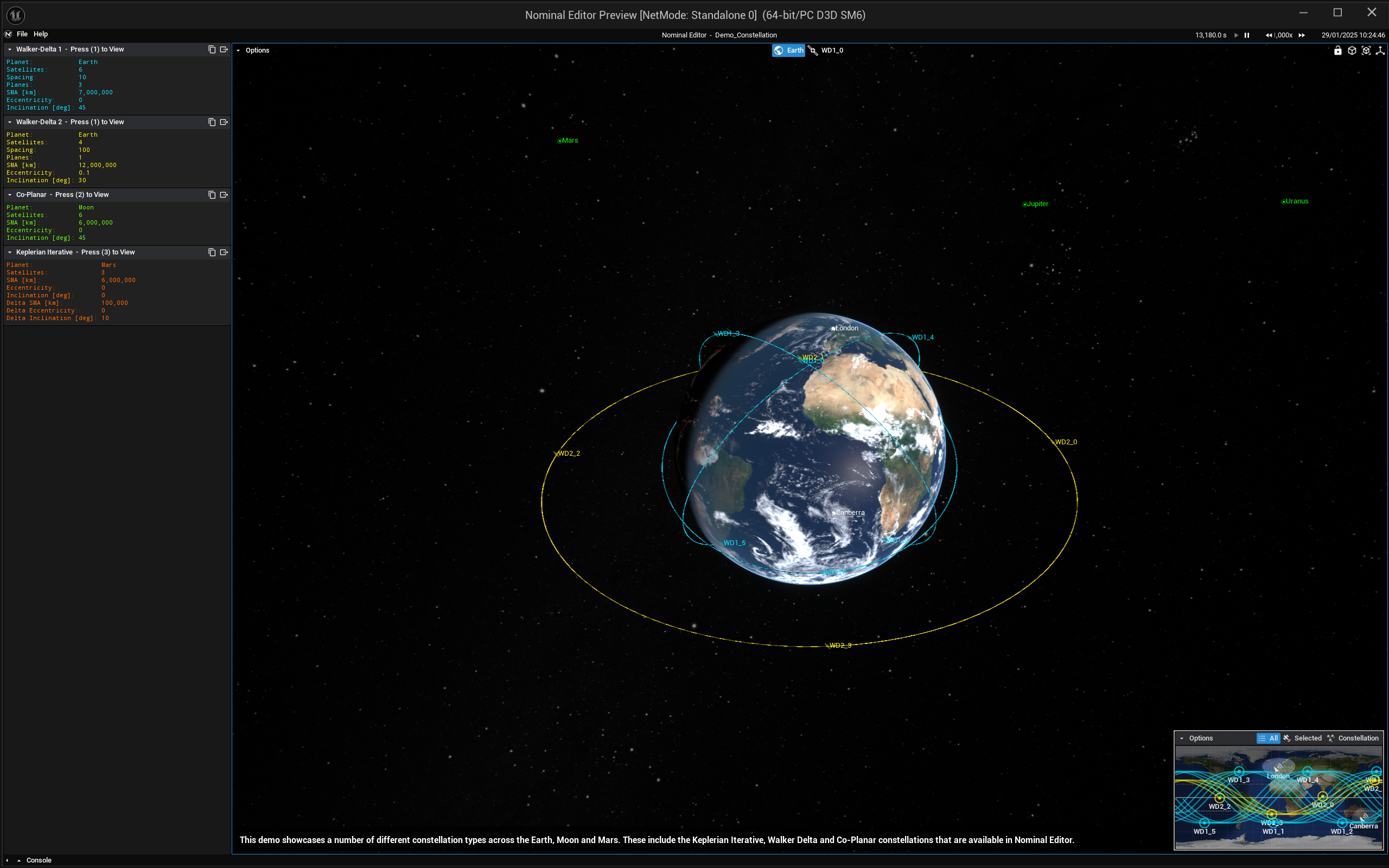
Two constellations initialized with the Walker-Delta constellation around the Earth will look something like the example demo with the constellations.
Coplanar Constellation
A Co-planer Constellation is a simple constellation where all the spacecrafts are on a single plane and evenly spaced out.
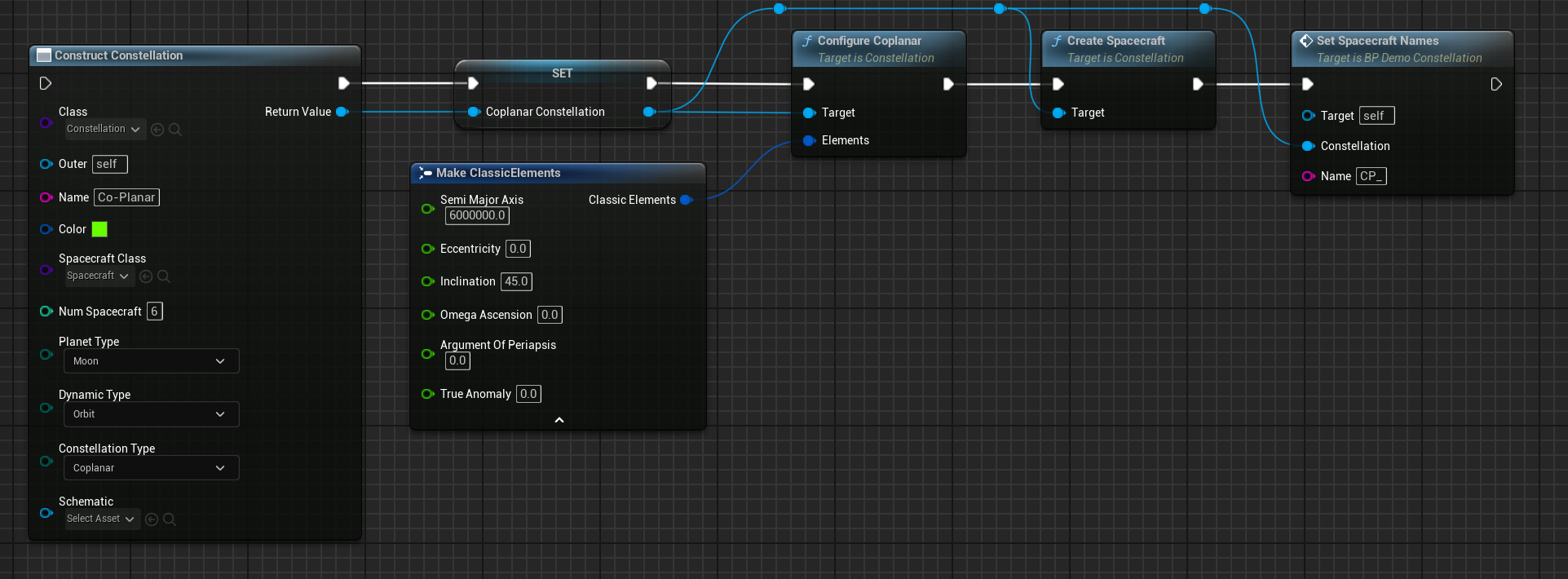
To create a Co-planar constellation, it is similarly created as the Walker-Delta constellation with a few changes:
- Change constellation type to Coplanar
- Use
Configure Coplanarfunction instead ofConfigure Walker Delta
To define the orbit of the constellation, use the classic elements properties of the Configure Coplanar. The parameters of classic elements are:
- Semi-Major Axis: The osculating semi-major axis of the orbit that will be applied to every spacecraft in the constellation.
- Inclination: The osculating inclination of the orbit that will be applied to every spacecraft in the constellation.
- Omega Ascension: The osculating Right Ascension of the Ascending Node that will be applied to the orbit of every spacecraft in the constellation.
- Omega Periapsis: The osculating argument of periapsis that will be applied to every spacecraft in the constellation.
- True Anom Ref: The starting osculating true anomaly of the reference spacecraft. The true anomaly of every other spacecraft will be equally spaced around the full orbit offset from the
True Anom Refvalue.
The blueprint functions would look similarly as the image below
A constellation initialized with the Coplanar constellation around the Moon will look something like the example demo with the constellations.
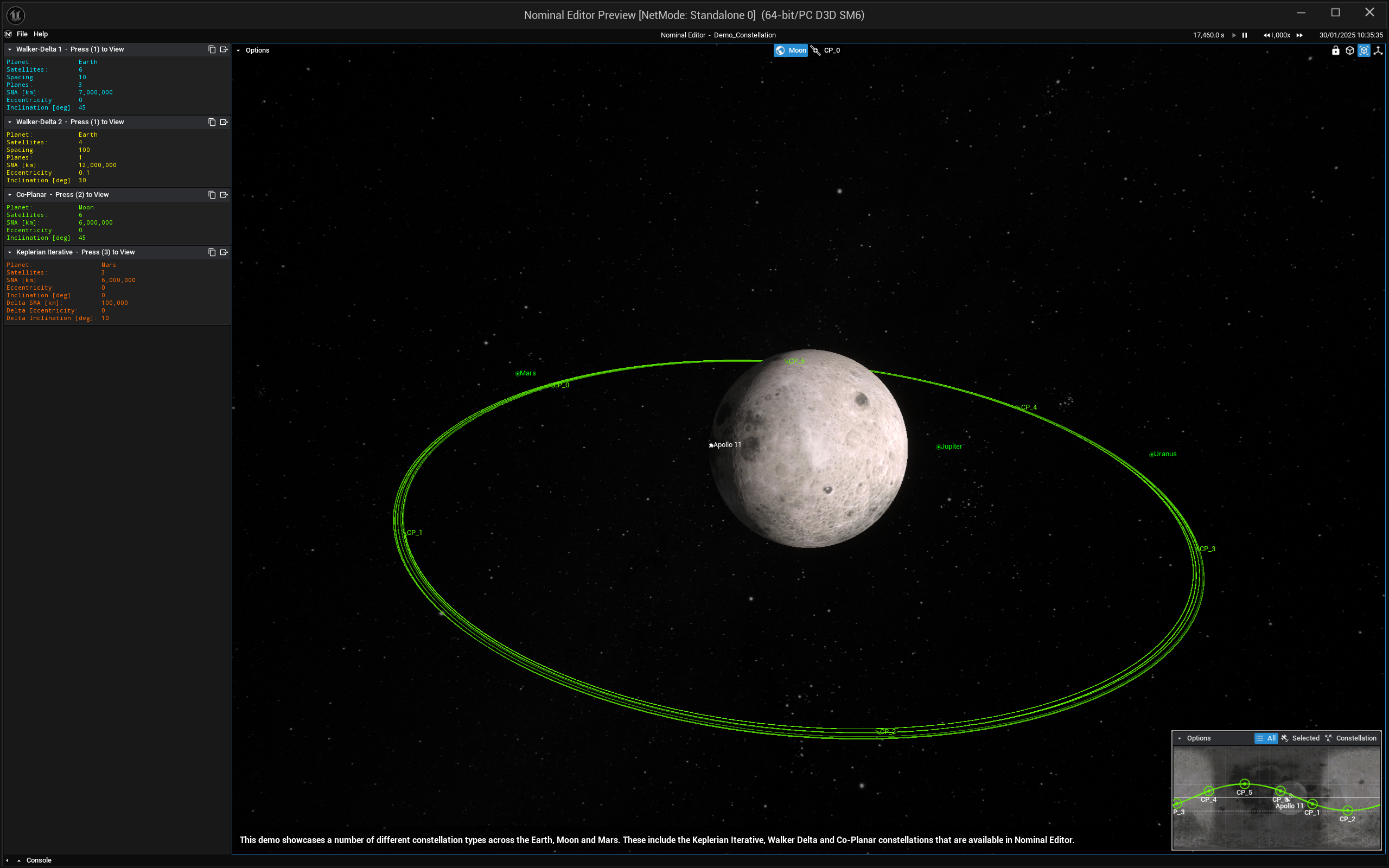
Keplerian Iterative Constellation
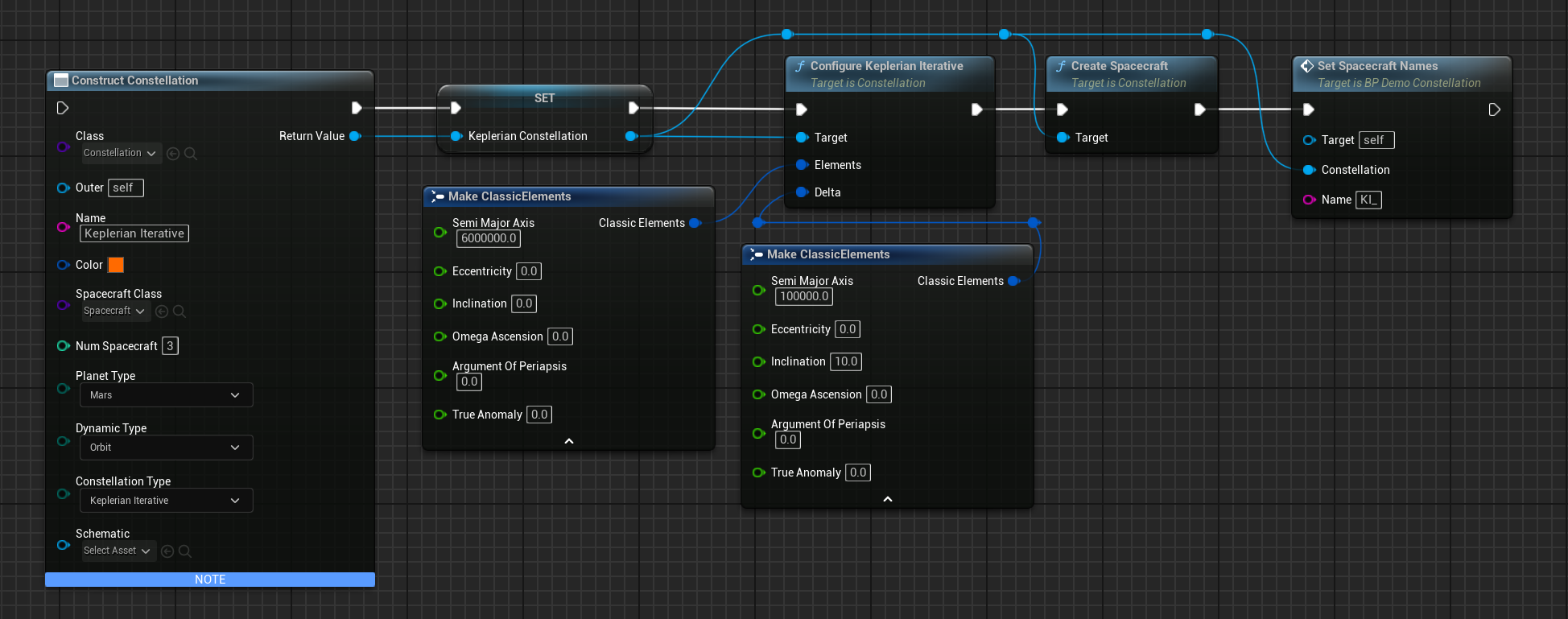
A Keplerian Iterative Constellation is a constellation where all the spacecrafts classic elements are spaced out by the classic elements specified. To create a Keplerian Iterative constellation, it is similarly created as the Walker-Delta constellation with a few changes:
- Change constellation type to Keplerian Iterative
- Use
Configure Keplerian Iterativefunction instead ofConfigure Walker Delta - Modify the Delta input in
Configure Keplerian Iterative. This controls how much does each spacecraft iterates on its classic element. E.g. a SMA of 1000m on the Delta would mean each spacecraft would be 1000m apart from the previous one.
The properties of the classic elements are the same as the Walker Delta and Coplanar. The elements in Configure Keplerian Iterative would affect the orbit of the first spaceraft while iterative would control how the spacing are between it and the previous spacecraft in the constellation.
- Semi-Major Axis: The osculating semi-major axis of the orbit that will be applied to every spacecraft in the constellation.
- Inclination: The osculating inclination of the orbit that will be applied to every spacecraft in the constellation.
- Omega Ascension: The osculating Right Ascension of the Ascending Node that will be applied to the orbit of every spacecraft in the constellation.
- Omega Periapsis: The osculating argument of periapsis that will be applied to every spacecraft in the constellation.
- True Anom Ref: The starting osculating true anomaly of the reference spacecraft. The true anomaly of every other spacecraft will be equally spaced around the full orbit offset from the
True Anom Refvalue.
The blueprint functions would look similarly as the image below
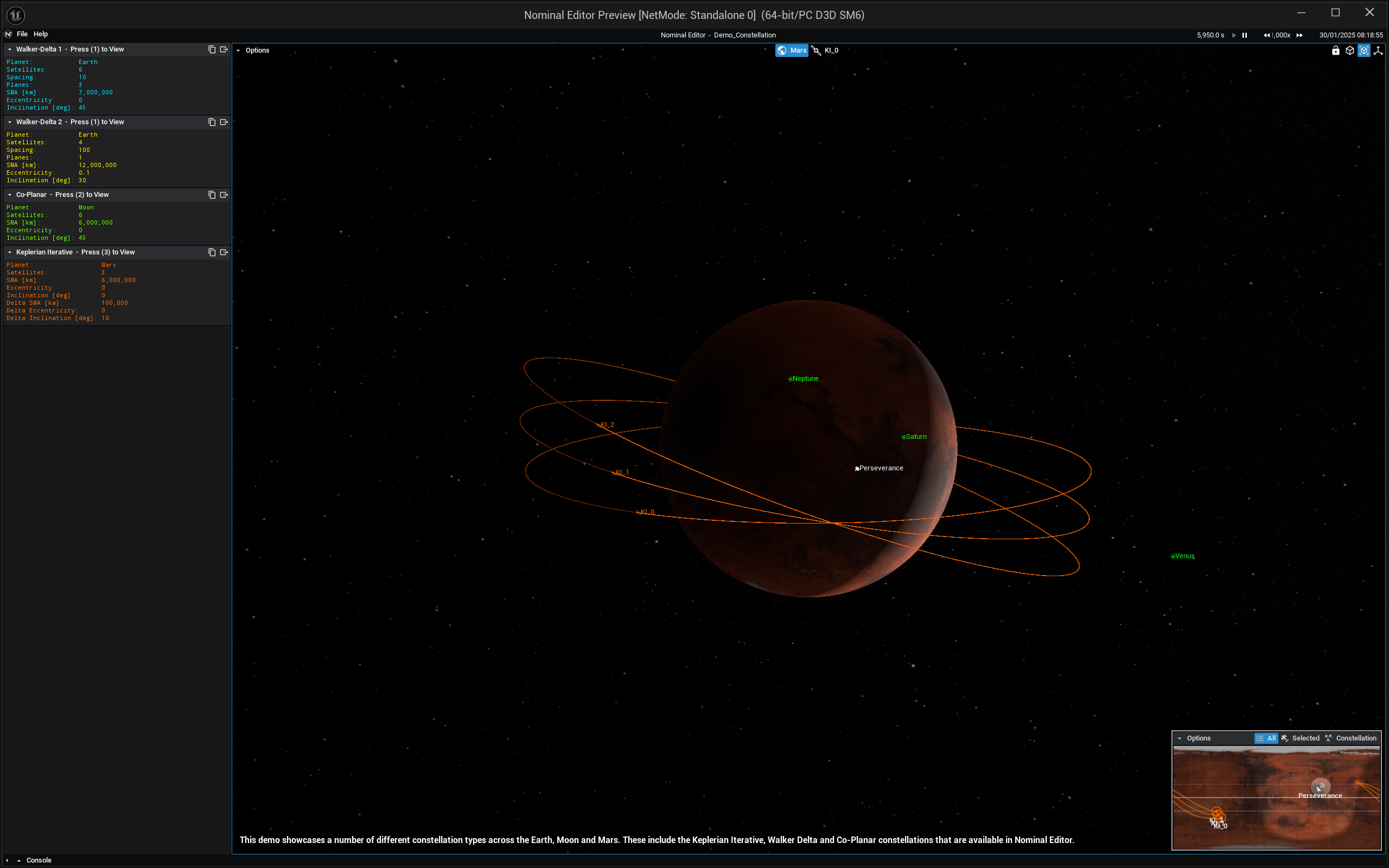
A constellation initialized with the Keplerian Iterative constellation around the Mars will look something like the example demo with the constellations.
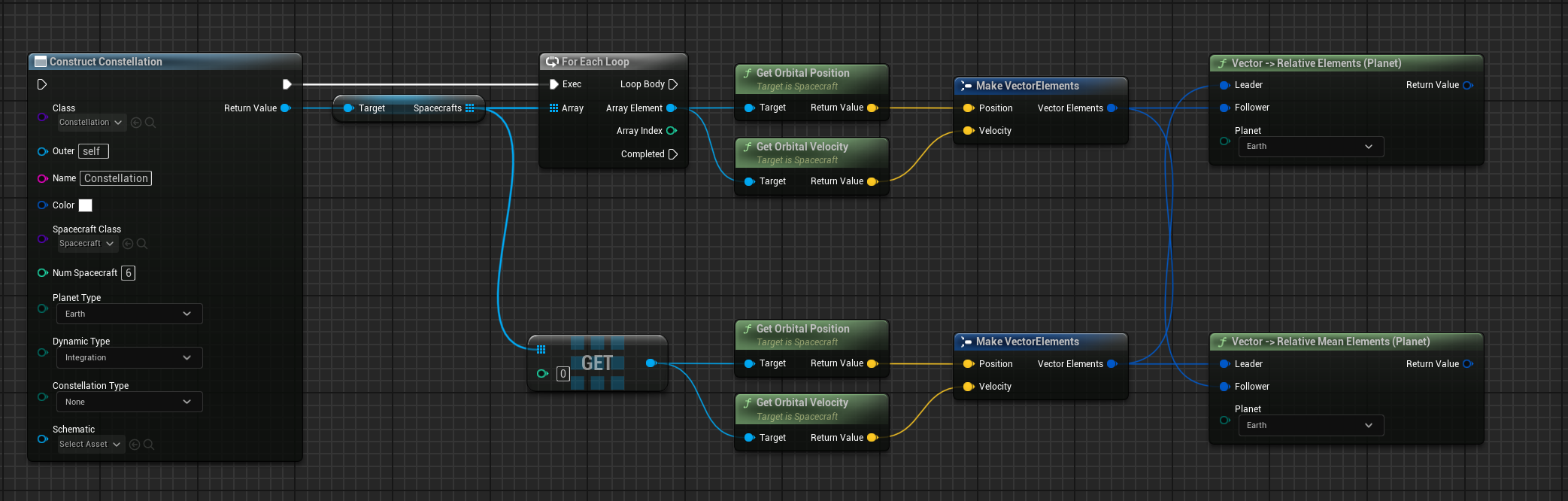
Measuring the Relative Orbital Elements
To calculate the relative osculating or relative mean orbital elements, use the Vector → Make Relative Elements (Planet) function. This function also has a reference to the planet being orbited to complete the conversion of absolute state to mean orbital elements and then to relative orbital elements. This function also takes the Inertial state vector of the spacecraft (Follower) and a corresponding reference spacecraft (Leader) in which its state is being measured relative to. The state vectors of the leader and follower spacecraft can be created by using the Get Position and Get Velocity functions in the spacecraft class.