Software: Reaction Wheel Null Space

Description

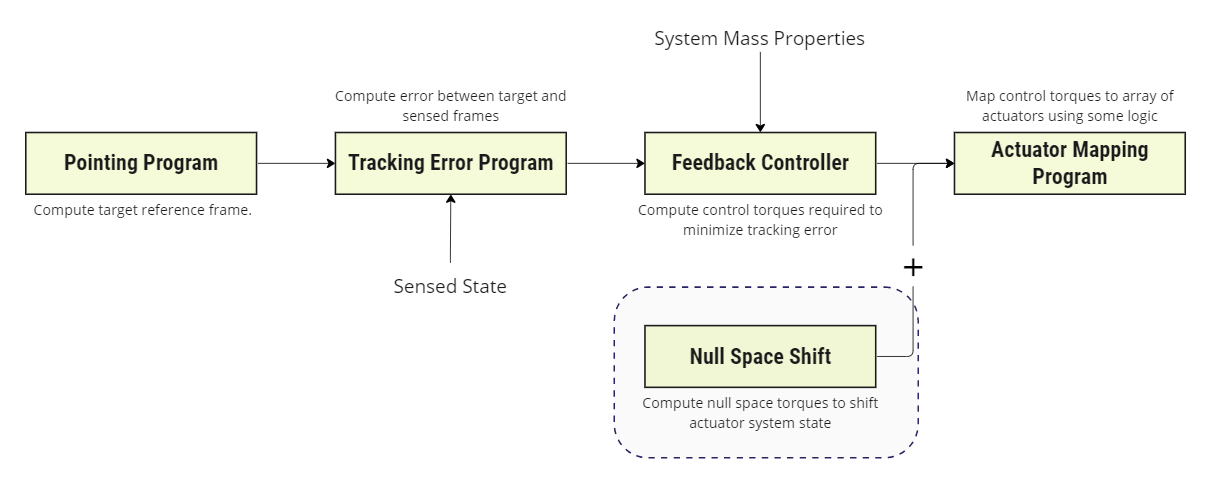
Figure 1: Application of a null-space program to perturb a control system

The purpose of this module is to reaction wheel speeds of an array to desired values by using the null space of the array i.e. changing wheel speeds while imparting no net torque to the spacecraft.

Example Use Cases

Drive Steady State RW Speed to Non-Zero Condition: Reaction wheels typically operate poorly near zero RPM. Use of a null space to drive reaction wheel speeds away from zero steady-state spin can improve pointing performance.

Module Implementation

Given an array of \(N\) reaction wheels, the steering matrix \([G_s]\) can be defined as,

\[ [G_s] = [\mathbf{\hat{g}}_{s,1},...,\mathbf{\hat{g}}_{s,N}] \]

The null motion projection matrix \([\tau]\) is given by [1],

\[ [\tau] = [I_{N\times N}] - [G_s]^T([G_s][G_s]^T)^{-1}[G_s] \]

This matrix will map any vector \(\mathbf{d}\) into the null-space of \([G_s]\) such that there is no net torque exerted on the system. To apply this to drive the reaction wheels to a desired spin rate \(\Omega_{i,d}\), we let the error between the measured \(\Omega_{i,m}\) and desired be,

\[ \Delta \Omega_{i} = \Omega_{i,m} - \Omega_{i,d} \]

We can then compute the desired torque vector \(\mu_{null}\) that minimizes \(\Delta \Omega\) for \(N\) wheels as,

\[ \mu_{null} = [\tau]\mathbf{d} = -[\tau]K\Delta\Omega \]

where \(K\) is a proportional gain term.

This torque can then be super-imposed on the control torque \(\mu_{cont}\) such that the total torque applied to the reaction wheel array is,

\[ \mu_s = \mu_{cont} + \mu_{null} \]

Assumptions/Limitations

This control approach assumes that the spacecraft angular accelerations are much less than the rotation rate of the wheels.

References