Software: Reaction Wheel Motor Voltage

Description

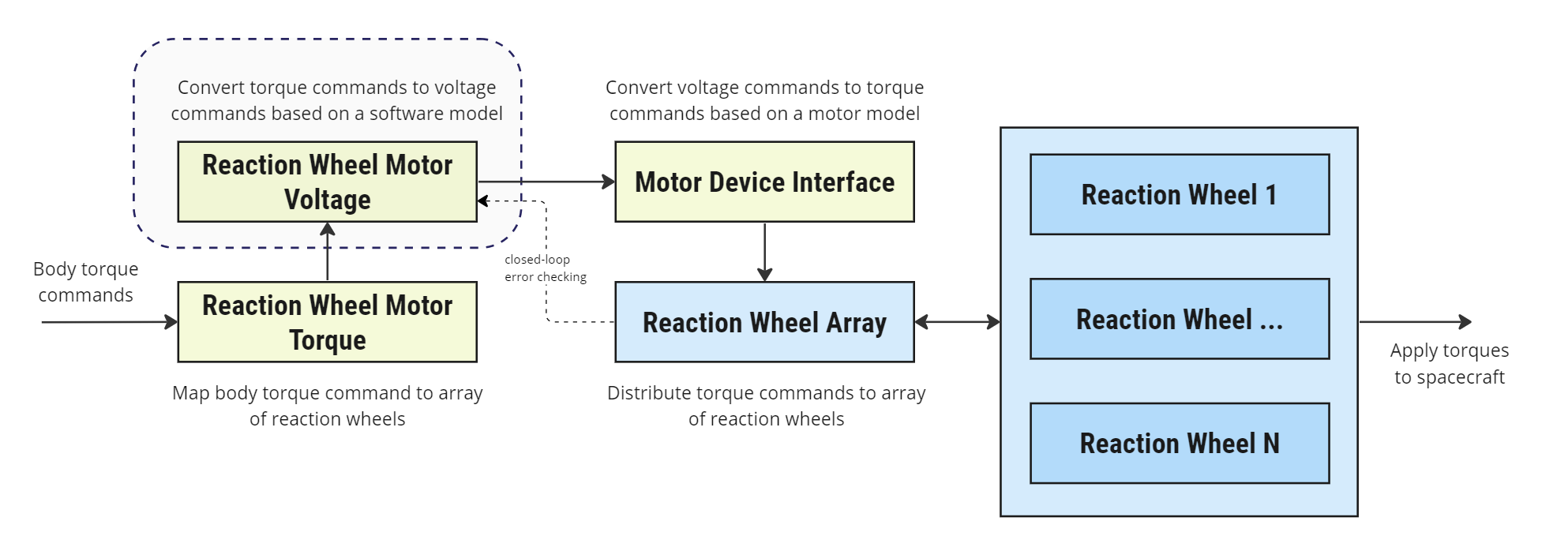
The purpose of this module is to map an array of reaction wheel command torques to equivalent voltage commands. These voltage commands would then interface with either an EPS sub-system or directly, as illustrated in the figure above, with a MotorDeviceInterface module. Similar to the ReactionWheelEncoder, this module simulates finite measurement errors (e.g. minimum and maximum thresholds) and a voltage dead-band, where control torques that map below \(|V_{min}|\) are zeroed. The model may also be run in a closed or open-loop mode (described below). The purpose of the closed-loop model is to provide a method to identify and correct for errors between reaction wheel responses and commands e.g. automatically correct for an unknown bias in a motor (which can be configured in the MotorDeviceInterface module).

Example Use Cases

• Add EPS-based controller to RW Array: This module provides a mechanism to interface the power interface (directly or indirectly) with the simulation command structure.
• Investigate resilience to pointing errors: By using closed-loop error tracking, this module can be used to investigate the impact of biases on pointing accuracy.

Module Implementation

Open Loop Voltage Conversion

Given a commanded \(\mu_s\), the voltage rate \(\alpha\) will be written as:

\[ \alpha = \frac{V_{max} - V_{min}}{\mu_{max}} \]

The output voltage is then:

\[ V(\mu_s) = \alpha \mu_s + |V_{min}| \text{sign}(\alpha \mu_s) \]

Closed-Loop Command Tracking

In this mode, the reaction wheel speed \(\Omega\) is monitored to see if the actual torque being applied matches the commanded torque. Given a known spin axis moment of inertia of the nth wheel \(J_n\), this can be written as:

\[ \mu_n = J_n \dot{\Omega}_n \]

The angular rate of the wheel is evaluated using a simple backward difference method.

\[ \dot{\Omega}_n = \frac{\Omega_n - \Omega_{n-1}}{\Delta t} \]

The closed feedback can be written as,

\[ \mu_{s,CL} = \mu_s - K(\mu_n-\mu_s) \]

Where \(K\) is a positive feedback gain. The closed loop command torque is then fed into the open loop voltage conversion equation.

References

[1] Hanspeter Schaub and John L. Junkins. Analytical Mechanics of Space Systems. AIAA Education Series, Reston, VA, 3rd edition, 2014.