Custom Components: Creating a Solar Panel
Custom Solar Panel
This example solar panel will be able to track the total amount of power produced over the lifetime of the simulation. This will be done by checking the power value of each frame after calculating it and summing up each value. Additionally, the efficiency of the solar panel will change based on the incident angle with the sun - when in full sunlight, the solar panel will decrease its efficiency when the solar panel is pointed away from the sun.
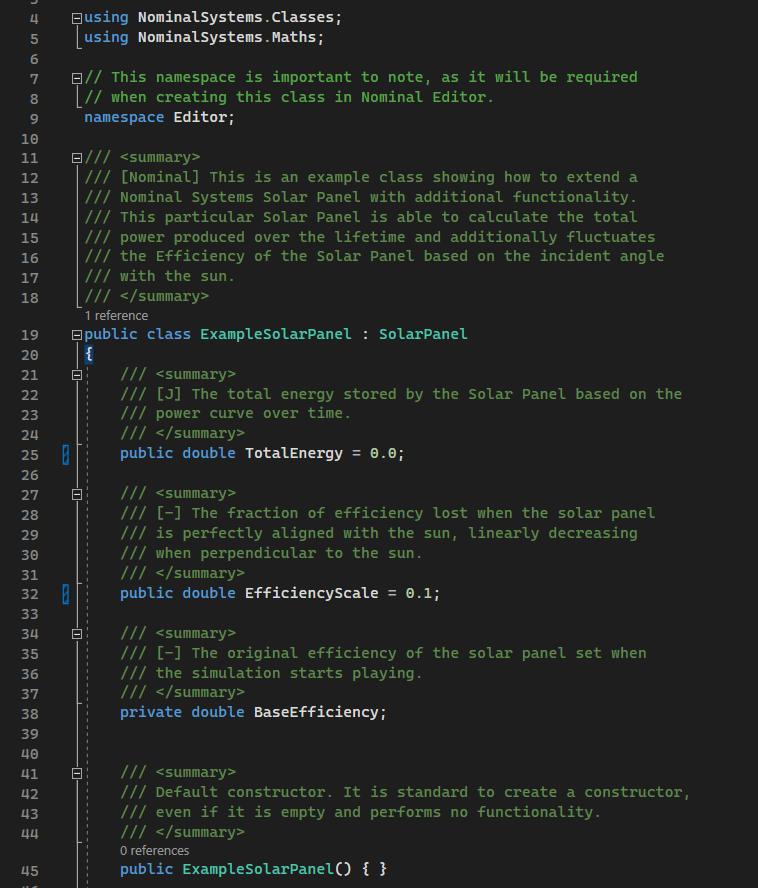
First, a parameter needs to be added to store the total energy that the solar panel has produced over time. This should be added within the class definition but outside of any functions. It is a public variable and, since it is numeric, should be of type double.
public double TotalEnergy = 0.0;
Note
C# standards use the upper-camel casing for their class-level fields, properties and methods. For local variables within functions, the lower-camel casing is used instead. It is also good practice to specify the access modifier out of public, private, protected and internal.
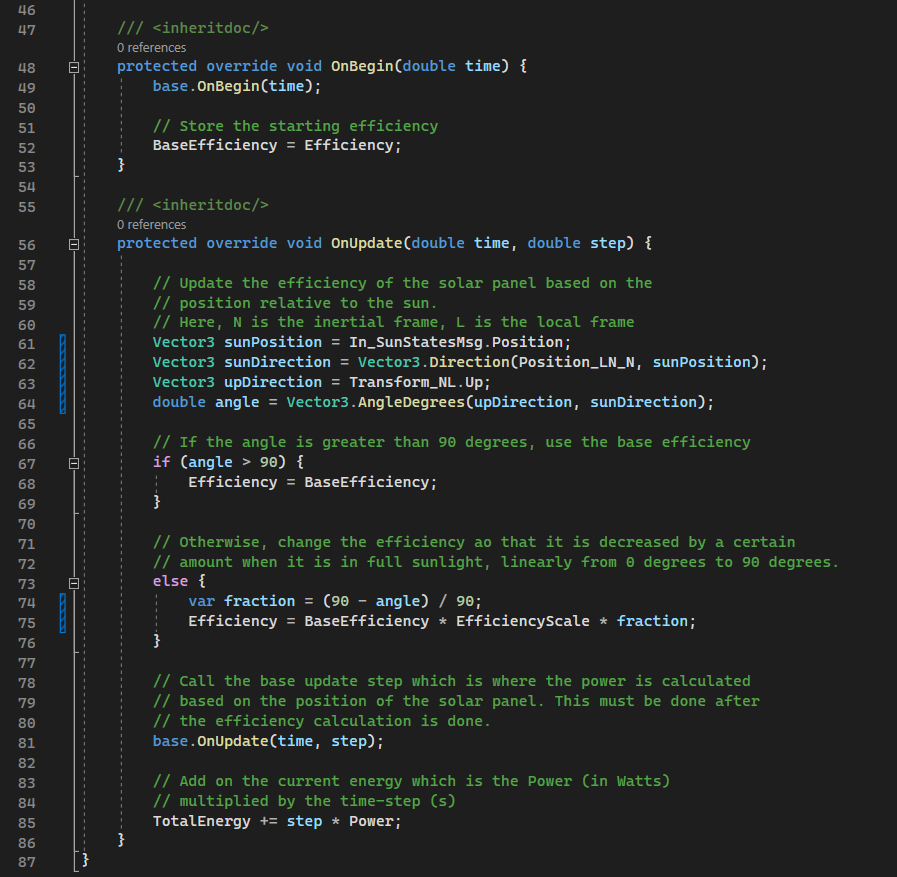
To calculate the total power, after the call to the base solar panel class that calculates the power of the solar panel, the total energy can be updated to add the power multiplied by the step. As power is in units of Watts, the energy is the multiplication of the power and time.
protected override void OnUpdate(double time, double step) {
base.OnUpdate(time, step);
TotalEnergy += step * Power;
}
Changing Efficiency
The next task is to change the efficiency of the solar panel and apply it before the update call to the solar panel. This ensures that the solar panel’s power is calculated with the updated efficiency. The first step is to determine the incident angle with the sun. To do this, we first need the direction of the sun. Nominal Systems classes use the NominalSystems.Maths classes for mathematical calculations, including Vector3 and Matrix3 classes, which define 3-part double vectors and 3x3 matrices respectively. This can be included using the code at the top of the script.
using NominalSystems.Maths;
Firstly, the position of the sun relative to the body can be calculated. The sun’s position can be found in the state message of the solar panel. The In_SunStatesMsg contains the SPICE body information about the sun and is already attached to the solar panel in the OnBegin event. This is an input message, meaning that the data is controlled by another component but this component has access to the data within the message, but should not write to it.
Vector3 sunPosition = In_SunStatesMsg.Position;
The position of the solar panel relative to the origin (which is the same frame that the sun object is in) can be found using the inherited property Position_LN_N. This is the position of the local object (L) relative to the inertial origin (N) in the inertial frame (N). The notation for some of the mathematical names can be confusing, but in this case, it is simply the full absolute position of the solar panel relative to the origin of the simulation (most likely the Earth’s centre in this case). Using the Vector3.Direction function, the direction between the sun and the solar panel can be calculated.
Vector3 sunDirection = Vector3.Direction(Position_LN_N, sunPosition);
This direction will be normalized and will be in the direction of the sun away from the solar panel. The next step is to calculate the pointing vector of the solar panel. In almost all components, the primary pointing axis is the Up axis, which is the direction relative to the coordinate system of the component in which the solar panel is able to receive power. This direction relative to the origin can be found using the Transform_NL, which is the transform of the component (L) in the inertial frame (N). Each component has a transform that contains the position and rotation of the object, stored in a 4x4 matrix. The position parameter before is simply pulled from the transform when accessed.
Vector3 upDirection = Transform_NL.Up;
To calculate the angle between the two vectors, we can use the dot product between the two. The general formula for calculating angles between vectors is:
assuming that the vectors \(\vec{a}\) and \(\vec{b}\) are normalized already. In this case, the direction vectors are normalized to have a magnitude of 1. The Vector3 class has a function that does this calculation for you and returns the angles in degrees.
double angle = Vector3.AngleDegrees(upDirection, sunDirection);
Before we check the angle and adjust the efficiency, if the angle is greater than 90 degrees, we want the efficiency to be the base efficiency of the component that was present when the component first started in the simulation. We can store this in a variable and set the value to the parameter of Efficiency in the OnBegin event.
private double BaseEfficiency;
...
protected override void OnBegin(double time) {
base.OnBegin(time);
BaseEfficiency = Efficiency;
}
Returning to the OnUpdate method, the angle can be checked to see if it is greater than 90 degrees. If it is, the efficiency of the solar panel should be returned to the base value.
if (angle > 90) {
Efficiency = BaseEfficiency;
}
If the angle is less than 90 degrees, the efficiency should be scaled to decrease by some amount. This will be calculated so that the efficiency when the panel is directly in line with the sun will have an efficiency of \(kE\), where \(E\) is the base efficiency and \(k\) is the parameter, which will have a value of EfficiencyScale. This will be set to 0.5 as the default value.
public double EfficiencyScale = 0.5;
...
protected override void OnUpdate(double time, double step) {
...
else {
var fraction = (90 - angle) / 90;
Efficiency = BaseEfficiency * (1 - EfficiencyScale * fraction);
}
base.OnUpdate(time, step);
}
Cleaning Up
That is all the code that is required for this particular component. Once done, the code should be cleaned up and comments should be added to explain what is happening. Commenting is recommended and small tips about what is happening at each stage should be added. The final code with comments will look like this: